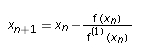Introduction
Newton's method is a technique for finding the root of a scalar-valued function f(x) of a single variable x. It has rapid convergence properties but requires that model information providing the derivative exists.
Background
Useful background for this topic includes:
- 3. Iteration
- 7. Taylor series
References
- Bradie, Section 2.4, Newton's Method, p.95.
- Mathews, Section 2.4, Newton-Raphson and Secant Methods, p.70.
- Weisstein, http://mathworld.wolfram.com/NewtonsMethod.html.
Theory
Assumptions
Newton's method is based on the assumption that functions with continuous derivatives look like straight lines when you zoom in closely enough to the functions. This is demonstrated here.
We will assume that f(x) is a scalar-valued function of a single variable x and that f(x) has a continuous derivative f(1)(x) which we can compute.
Derivation
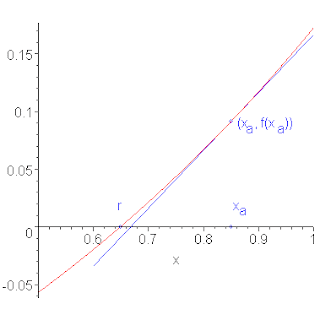
Suppose we have an approximation xa to a root r of f(x), that is, f(r) = 0. Figure 1 shows a function with a root and an approximation to that root.
Figure 1. A function f(x), a root r, and an approximation to that root xa.
Because f(x) has a continuous derivative, it follows that at any point on the curve of f(x), if we examine it closely enough, that it will look like a straight line. If this is the case, why not approximate the function at (xa, f(xa)) by a straight line which is tangent Txa to the curve at that point? This is shown in Figure 2.
Figure 2. The line tangent to the point (xa, f(xa)).
The formula for this line may be deduced quite easily: the linear polynomial f(1)(xa) ⋅ (x - xa) is zero at xa and has a slope of f(1)(xa), and therefore, if we add f(xa), it will be tangent to the given point on the curve, that is, the linear polynomial
is the tangent line. Because the tangent line is a good approximation to the function, it follows that the root of the tangent line should be a better approximation to the root than xa, and solving for the root of the tangent is straight-forward:
HOWTO
Problem
Given a function of one variable, f(x), find a value r (called a root) such that f(r) = 0.
Assumptions
We will assume that the function f(x) is continuous and has a continuous derivative.
Tools
We will use sampling, the derivative, and iteration. Information about the derivative is derived from the model. We use Taylor series for error analysis.
Initial Requirements
We have an initial approximation x0 of the root.
Iteration Process
Given the approximation xn, the next approximation xn + 1 is defined to be
Halting Conditions
There are three conditions which may cause the iteration process to halt:
- We halt if both of the following conditions are met:
- The step between successive iterates is sufficiently small, |xn + 1 - xn| < εstep, and
- The function evaluated at the point xn + 1 is sufficiently small, |f(xn + 1)| < εabs.
- If the derivative f(1)(xn) = 0, the iteration process fails (division-by-zero) and we halt.
- If we have iterated some maximum number of times, say N, and have not met Condition 1, we halt and indicate that a solution was not found.
If we halt due to Condition 1, we state that xn + 1 is our approximation to the root.
If we halt due to either Condition 2 or 3, we may either choose a different initial approximation x0, or state that a solution may not exist.
Error Analysis
Given that we are using Newton's method to approximate a root of the function f(x).
Suppose we have an approximation of the root xn which has an error of (r - xn). What is the error of the next approximationxn + 1 found after one iteration of Newton's method?
Suppose r is the actual root of f(x). Then from the Taylor series, we have that:
where ξ ∈ [r, xn]. Note, however, that f(r) = 0, so if we set the left-hand side to zero and divide both sides by f(1)(xn), we get:
We can bring the first two terms to the left-hand side and multiple each side by -1. For the next step, I will group two of the terms on the terms on the left-hand side:
Note that the object in the parentheses on the left-hand side is, by definition, xn + 1 (after all, xn + 1 = xn - f(xn)/f(1)(xn) ), and thus we have:
But the left hand side is the error of xn + 1, and therefore we see that error is reduced by a scalar multiple of the square of the previous error.
To demonstrate this, let us find the root of f(x) = ex - 2 starting with x0 = 1. We note that the 1st and 2nd derivatives of f(x) are equal, so we will approximate ½ f(2)(ξ)/f(1)(xn) by ½. Table 1 shows the Newton iterates, their absolute errors, and the approximation of the error based on the square previous error.
Table 1. Newton iterates in finding a root of f(x) = ex - 2.
| n | xn | errn = ln(2) - xn | ½ errn - 12 |
|---|---|---|---|
| 0 | 1.0 | -3.069 ⋅ 10-1 | N/A |
| 1 | 0.735758882342885 | -4.261 ⋅ 10-2 | -4.708 ⋅ 10-2 |
| 2 | 0.694042299918915 | -8.951 ⋅ 10-4 | -9.079 ⋅ 10-4 |
| 3 | 0.693147581059771 | -4.005 ⋅ 10-7 | -4.006 ⋅ 10-7 |
| 4 | 0.693147180560025 | -8.016 ⋅ 10-14 | -8.020 ⋅ 10-14 |
Note that the error at the nth step is very closely approximated by the error of the (n - 1)th step. Now, in reality, we do not know what the actual error is (otherwise, we wouldn't be using Newton's method, would we?) but this reassures us that, under reasonable conditions, Newton's method will converge very quickly.
Failure of Newton's Method
The above formula suggests that there are three situations where Newton's method may not converge quickly:
- Our approximation is far away from the actual root,
- The 2nd derivative is very large, or
- The derivative at xn is close to zero.
Examples
Example 1
As an example of Newton's method, suppose we wish to find a root of the function f(x) = cos(x) + 2 sin(x) + x2. A closed form solution for x does not exist so we must use a numerical technique. We will use x0 = 0 as our initial approximation. We will let the two values εstep = 0.001 and εabs = 0.001 and we will halt after a maximum of N = 100 iterations.
From calculus, we know that the derivative of the given function is f(1)(x) = -sin(x) + 2 cos(x) + 2x.
We will use four decimal digit arithmetic to find a solution and the resulting iteration is shown in Table 1.
Table 1. Newton's method applied to f(x) = cos(x) + 2 sin(x) + x2.
| n | xn | xn + 1 | |f(xn + 1)| | |xn + 1 - xn| |
|---|---|---|---|---|
| 0 | 0.0 | -0.5000 | 0.1688 | 0.5000 |
| 1 | -0.5000 | -0.6368 | 0.0205 | 0.1368 |
| 2 | -0.6368 | -0.6589 | 0.0008000 | 0.02210 |
| 3 | -0.6589 | -0.6598 | 0.0006 | 0.0009 |
Thus, with the last step, both halting conditions are met, and therefore, after four iterations, our approximation to the root is -0.6598 .
Questions
Question 1
Find a root of the function f(x) = e-x cos(x) starting with x0 = 1.3 . The terminating conditions are given by εabs = 1e-5 and εstep = 1e-5.
Answer: 1.57079632679490 after five iterations.
Question 2
Perform three steps of Newton's method for the function f(x) = x2 - 2 starting with x0 = 1. Use a calculator for the third step.
Answer: 3/2, 17/12, 577/408 ≈ 1.414215686274510
Applications to Engineering
Consider the circuit, consisting of a voltage source, a resistor, and a diode, shown in Figure 1.
Suppose we wish to find the current running through this circuit. To do so, we can use Kirchhoff's voltage law (KVL) which says that the sum of the voltages around a loop is zero. For this, we need the model of diode which states that the relationship between the current and the voltage across a diode is given by the equation
Solving this equation for the voltage v and using values IS = 8.3e-10 A, VT = 0.7 V, and n = 2, we get from KVL that
This equation cannot be solved exactly for the current with any of the tools available in an undergraduate program (it requires the use of the Lambert W function). Therefore we must resort to using numerical methods:
Defining the left hand side of the equation to be v(i), we have to solve v(i) = 0 for i, and we will continue iterating until εstep< 1e-10 and εabs < 1e-5.Table 1. Newton's method applied to v(i).
| n | in | in + 1 | |v(in + 1)| | |in + 1 - in| |
|---|---|---|---|---|
| 0 | 0.0 | 2.964283918e-10 | 0.0724 | 2.96e-10 |
| 1 | 2.964283918e-10 | 3.547336588e-10 | 1.81e-3 | 5.83e-11 |
| 2 | 3.547336588-10 | 3.562680160-10 | 1.17e-5 | 1.53e-12 |
| 3 | 3.562680160e-10 | 3.562690102e-10 | 2.63e-9 | 9.94e-16 |
Therefore, the current is approximately 3.562690102e-10 A.
Matlab
Finding a root of f(x) = cos(x):
eps_step = 1e-5;
eps_abs = 1e-5;
N = 100;
x = 0.2;
for i=1:N
xn = x - cos(x)/( -sin(x) );
if abs( x - xn ) < eps_step && abs( cos( xn ) ) < eps_abs
break;
elseif i == N
error( 'Newton\'s method did not converge' );
end
x = xn;
end
xn
What happens if you start with smaller values of x? Why?
Maple
The following commands in Maple:
with( Student[Calculus1] ): NewtonsMethod( cos(x), x = 0.5, output = plot, iterations = 5 );
produces the plot in Figure 1:
?NewtonsMethod
?Student , Calculus1